Atividade 14: O cartógrafo pobre – Colorindo mapas

Apresentação

Muitos problemas de optimização envolvem situações em que certos eventos não podem acontecer ao mesmo tempo, ou certos membros de um conjunto de objetos não podem ser adjacentes. Por exemplo, qualquer um que tentou organizar sua agenda de aulas e reuniões terá se deparado com o problema de satisfazer as restrições de todas as pessoas envolvidas. Muitas dessas dificuldades ficam claras no problema de colorir o mapa, no qual as cores devem ser escolhidas para os países do mapa de forma que países vizinhos tenham cores diferentes. Esta atividade é sobre este problema.

Disciplinas e conteúdos relacionados

Habilidades

Nível de Ensino

Material

Cada aluno precisará de:

Colorindo mapas

Essa atividade gira em torno de uma história na qual os alunos foram solicitados a ajudar um cartógrafo, que está colorindo os países em um mapa. Não importa qual é a cor de cada país, contanto que seja diferente da de todos os países vizinhos.

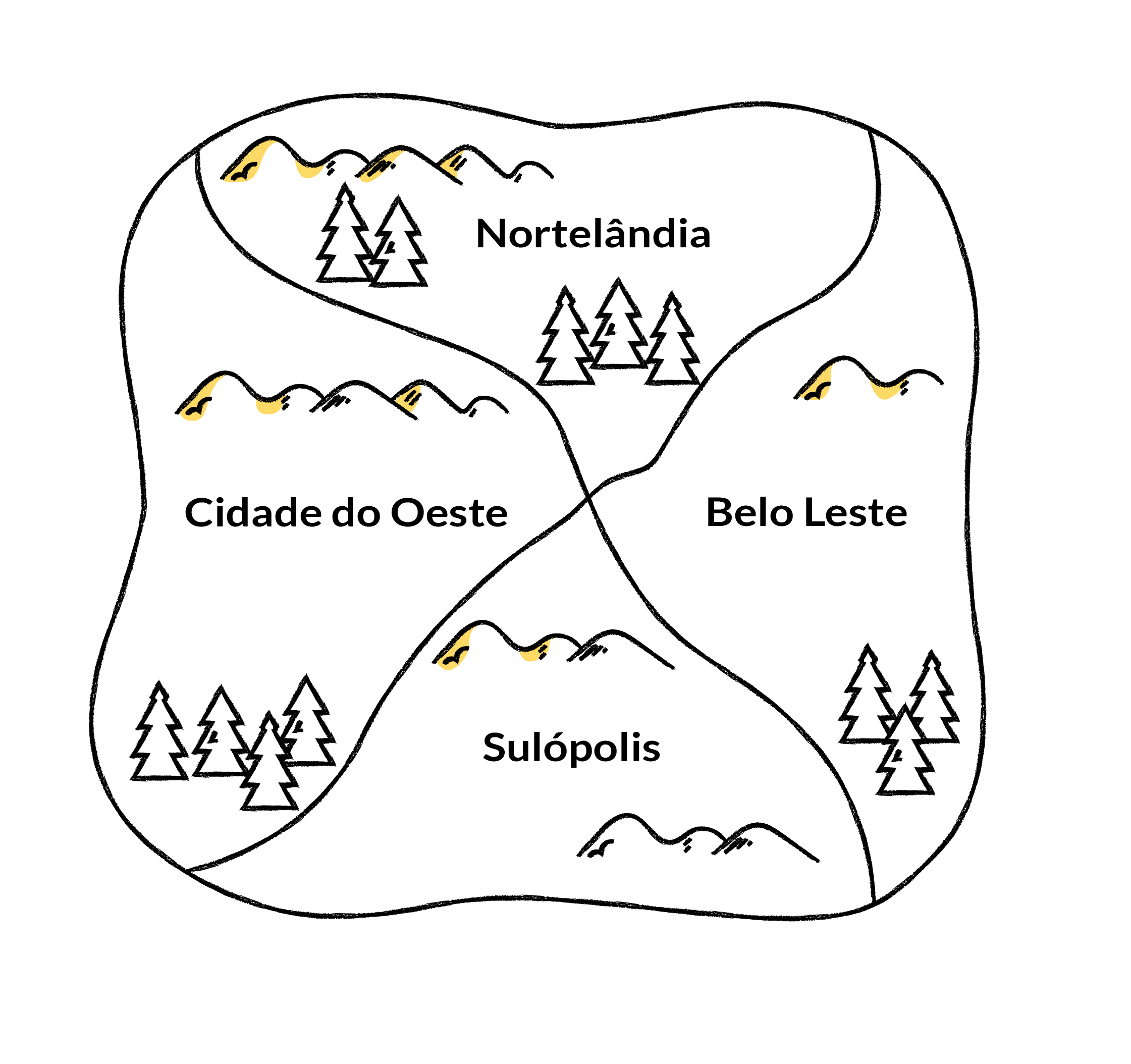
Por exemplo, o mapa abaixo mostra quatro países. Se colorirmos Nortelândia de vermelho, então Oestelândia e Lestelândia não podem ser vermelhas, já que seria difícil enxergar as suas respectivas fronteiras com Nortelândia. Nós poderíamos colorir Oestelândia de verde, e também seria aceitável colorir Lestelândia de verde porque esses países não dividem fronteira. (Se dois países tem apenas um ponto de fronteira em comum, eles não contam como vizinhos e assim podem ser da mesma cor.) Sulândia pode ser pintado de vermelho e desta forma só precisaremos de duas cores para o mapa.

Na nossa história, o cartógrafo é pobre e não pode bancar muitos gizes de cera, então a ideia é usar a menor quantidade possível deles.

Discussão

Descreva o problema que os alunos trabalharão, demonstrando na lousa o processo de colorir os países.

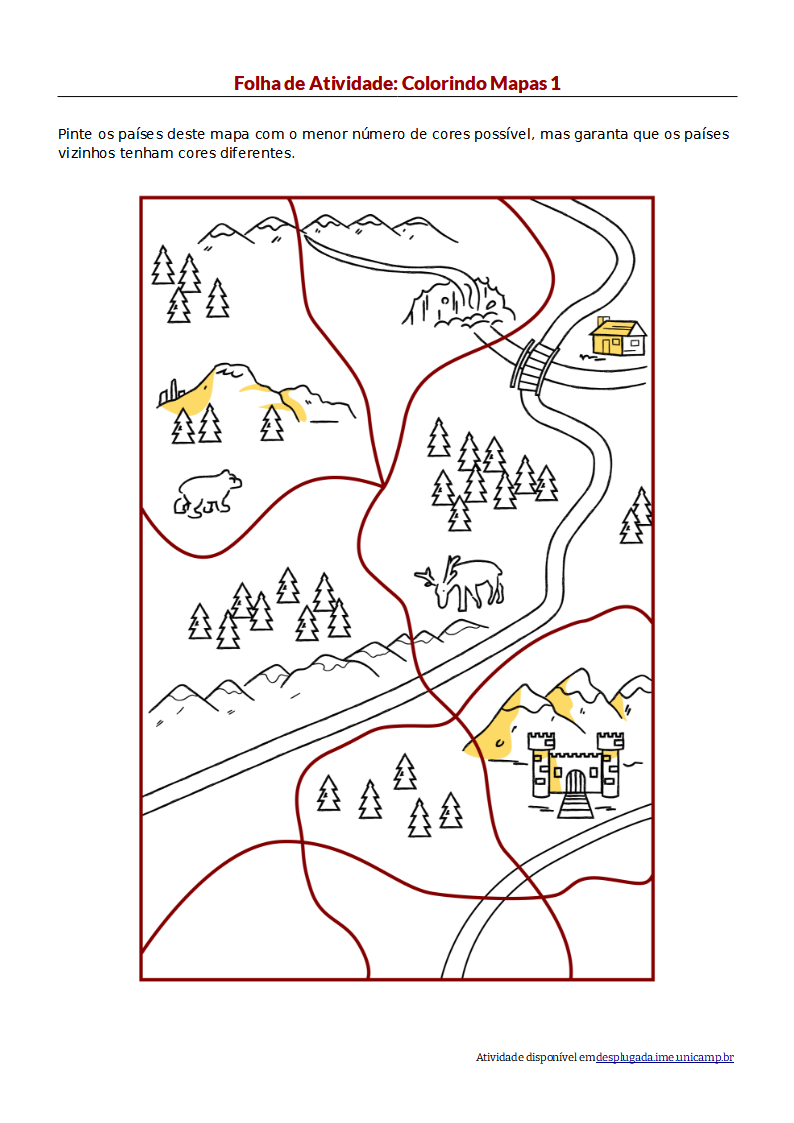
Distribua uma cópia da primeira folha de atividades. Este mapa pode ser colorido corretamente usando apenas duas cores. Embora restringir o número de cores a dois possa parecer particularmente desafiador, a tarefa é simples comparada com mapas que requerem mais cores porque existem poucas opções de cores que cada país pode ter.

Faça os alunos tentarem colorir o mapa com apenas duas cores. No processo, talvez eles descubram a regra: uma vez que um país é pintado de uma cor, qualquer país vizinho deve ser da segunda cor. Essa regra é aplicada repetidamente até que todos os países tenham sido coloridos. É melhor que os alunos descubram essa regra eles mesmos, ao invés dela ser dita a eles, uma vez que isso os dará uma ideia melhor do processo.

Assim que os estudantes terminarem cada exercício, pode-se entregar a eles a próxima folha de atividades para tentarem.

Os alunos podem perceber que é melhor usar algo para marcar as cores, como as fichas de pôquer coloridas, ao invés de colorir os países imediatamente, já que isso facilita para eles a mudança de ideia.

Para os alunos mais velhos, peça que expliquem como eles sabem que encontraram o menor número possível de cores. Por exemplo, são necessárias pelo menos três cores para este mapa porque ele contém três países que são vizinhos um a um.

Se alguns alunos terminarem todas as atividades cedo, peça a eles que façam um mapa que precisa de cinco cores. É comprovado que qualquer mapa pode ser colorido com apenas quatro cores, então isso deve mantê-los ocupados por algum tempo! Na nossa experiência os alunos irão encontrar rapidamente mapas que eles acreditam requerer cinco cores, mas é claro que sempre será possível encontrar uma solução com quatro cores para o mapa deles.

Variações e Extensões

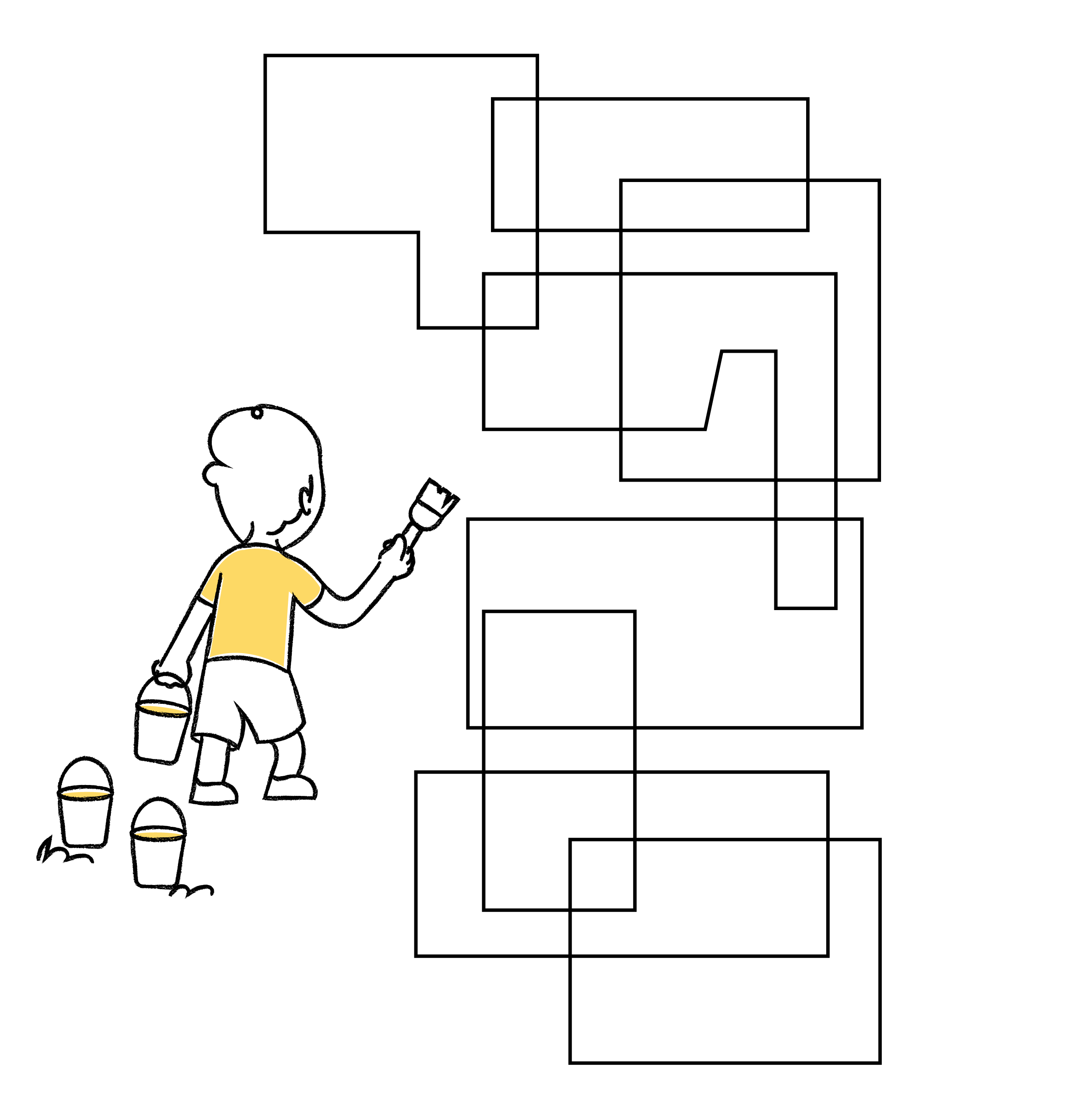
Existe uma forma simples de construir mapas que exigem apenas duas cores, como o mostrado abaixo. Este mapa foi desenhado sobrepondo curvas fechadas (linhas cujo começo emenda com o seu final). Você pode desenhar qualquer quantidade dessas curvas, de qualquer forma, uma sobre a outra, e você sempre acabará com um mapa que pode ser colorido com apenas duas cores. Os alunos podem tentar criar este tipo de mapa.

Quatro cores sempre são suficientes para colorir um mapa desenhado em um papel ou em uma esfera (isto é, o globo). Alguém pode se perguntar (como cientistas são pagos para fazer) quantas cores são necessárias para colorir mapas em superfícies mais estranhas, como um toro (o formato do donuts). Neste caso, os alunos podem querer fazer testes com isso.

Existem muitas outras variações divertidas do problema de colorir mapas que guiam em direções em que muita coisa é desconhecida. Por exemplo, se eu estou colorindo um mapa numa folha de papel eu saberei que, se eu for esperto, quatro cores serão suficientes. Mas suponha que, ao invés de colorir sozinho, eu estou colorindo com um colega incompetente (ou até mesmo adversário) e nós estamos nos revezando na escolha da cor de cada país. Assuma que eu escolho de maneira esperta, enquanto o meu colega escolhe de forma “permitida” enquanto nos revezamos colorindo países no mapa. Quantos gizes de cera precisam estar sobre a mesa para que eu, em minha esperteza, possa compensar o trabalho permitido, mas não muito inteligente (ou até mesmo subversivo) do meu colega? O número máximo não é conhecido! Em 1992 foi demonstrado que 33 gizes sempre serão suficientes, e em 2008 isso foi aperfeiçoado pela prova de que 17 gizes seriam o bastante, no entanto nós ainda não sabemos se essa quantia seria realmente requerida em algum caso. (Especialistas conjecturam que menos de 10 cores seriam suficientes). Os alunos podem gostar de encenar esta situação, que pode ser feita como um jogo de duas pessoas em que você tenta maximizar a quantidade de cores que o seu oponente precisa.

Em outra variação de Colorindo Mapas conhecida como Colorindo Impérios, nós começamos com dois mapas diferentes em duas folhas diferentes com o mesmo número de países. Cada país no mapa (podendo ser a Terra) está relacionado com outro país em outro mapa (que pode ser de colônias na Lua). Além do requisito do problema usual de colorir mapas de cores diferentes para países vizinhos, nós adicionamos o requisito de que cada país na Terra deve ser pintado da mesma cor que o seu correspondente na Lua. Quantas cores precisamos para esse problema? Atualmente a resposta não é conhecida.

Folhas de Atividades e Materiais Adicionais

Você também pode baixar todas as folhas de atividade e materiais adicionais em formato editável aqui.

Do que se trata tudo isso?

O problema de colorir o mapa explorado nesta atividade tem o objetivo essencial de encontrar o menor número de cores – duas, três ou quatro – necessárias para colorir determinado mapa. A hipótese de que qualquer mapa pode ser colorido usando apenas quatro cores foi formulada em 1852, mas não foi provada antes de 1976. A ciência da computação é repleta de problemas não solucionados, e saber que o teorema das quatro cores foi comprovado depois de mais de 120 anos de atenção dos pesquisadores é um estímulo a aqueles que trabalham outros problemas cuja solução tem sido incompreensível por décadas.

Colorir mapas pertence a uma classe geral de problemas conhecidos como “colorir grafos”. Na ciência da computação um grafo é uma representação abstrata de relações, como mostrado aqui.

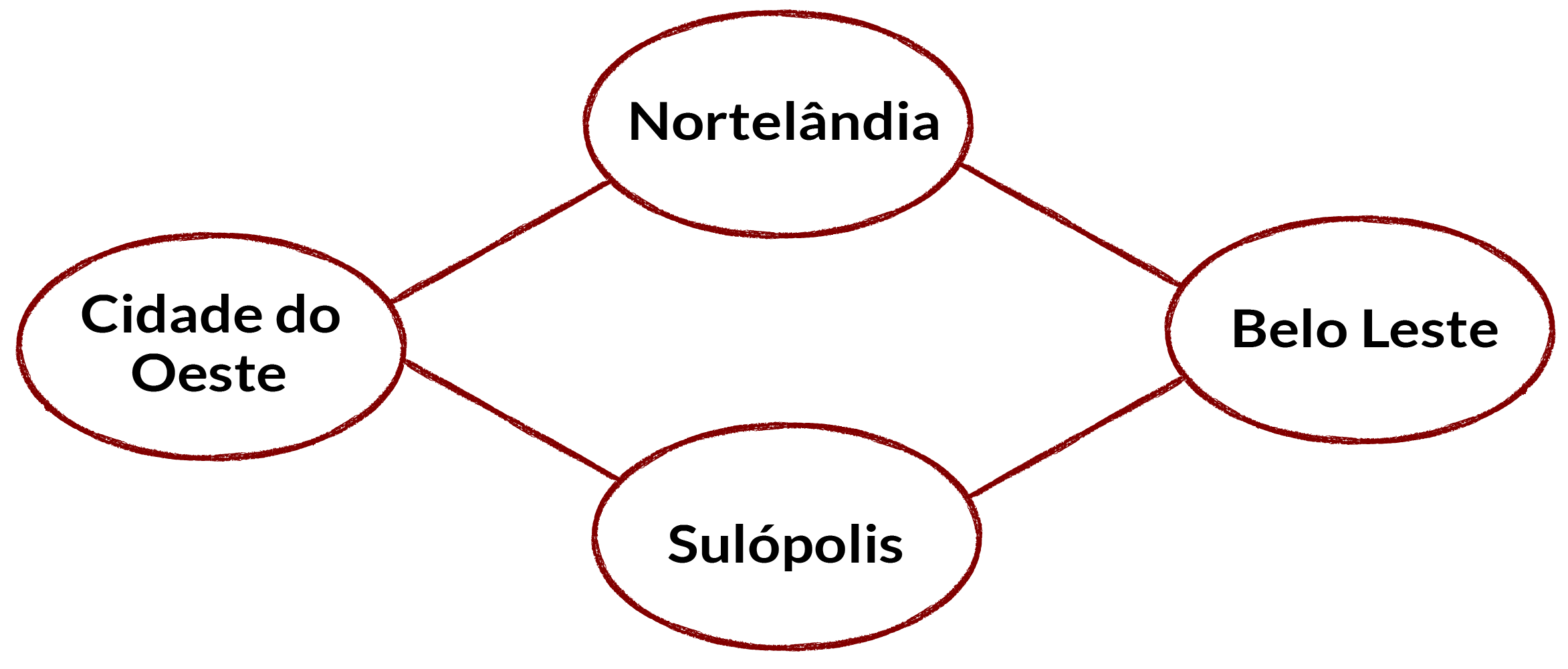
Conforme mencionado na Atividade 9 – A cidade enlameada, na ciência da computação, grafos são desenhados usando círculos, chamados “nós”, denotando objetos com linhas entre eles para indicar algum tipo de relação. O grafo abaixo representa o mapa do começo dessa atividade. Os nós representam os países e as linhas entre dois nós indicam que esses dois países tem uma fronteira em comum. No grafo, a regra para colorir é que nenhum par de nós conectados entre si deve ter a mesma cor. Ao contrário do mapa, não existe um número limite de cores que um grafo pode precisar, porque muitas restrições diferentes podem ser desenhadas como linhas conectando países, enquanto a natureza bidimensional dos mapas restringe os arranjos possíveis. O “problema de colorir grafos“ procura o menor número de cores necessárias para um grafo específico.

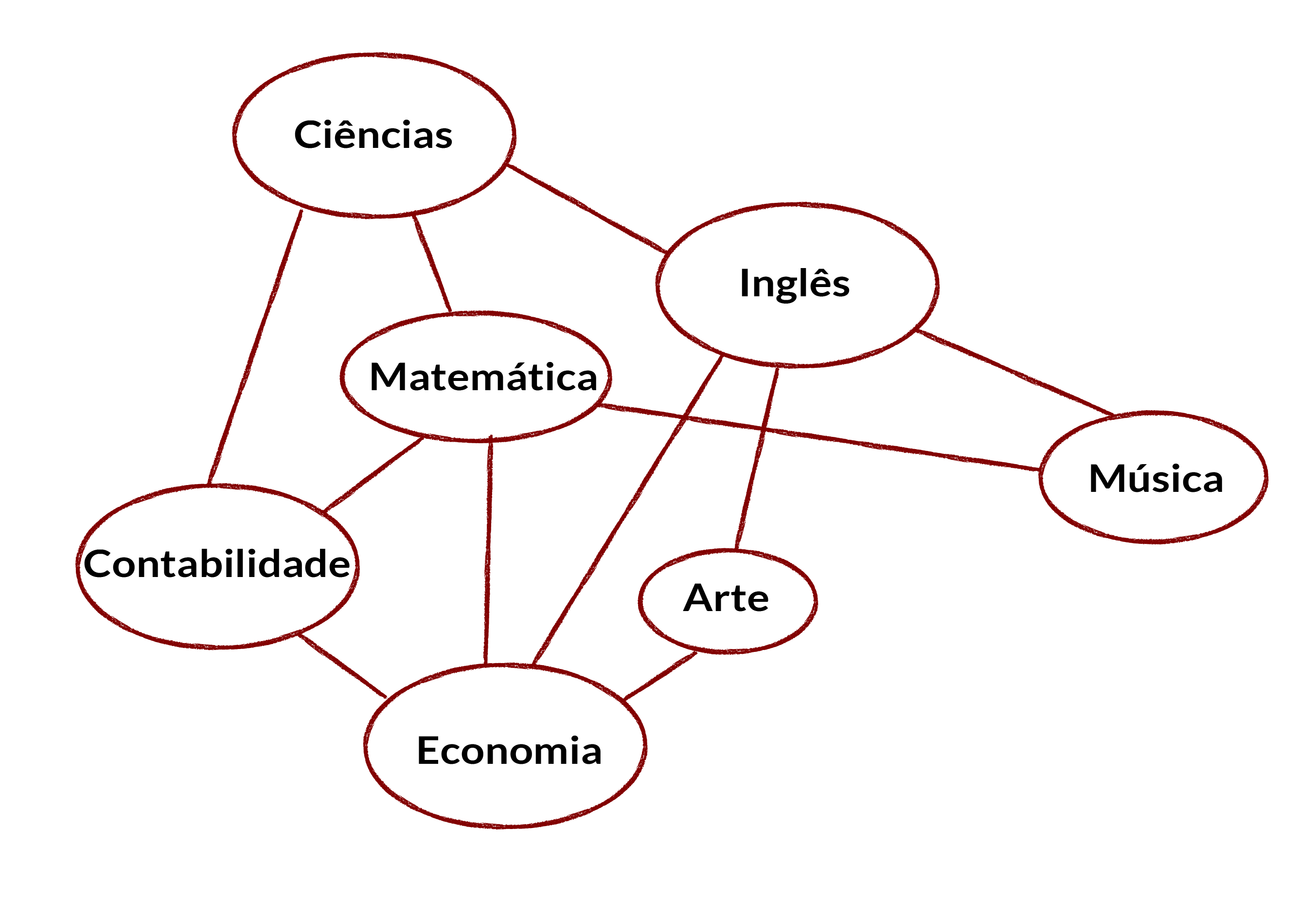
No grafo abaixo os nós correspondem a matérias escolares. A linha entre duas matérias indica que pelo menos um aluno está cursando ambas as matérias, então elas não devem ser agendadas para o mesmo horário. Usando essa representação o problema de agendar as aulas com a menor quantidade de horários diferentes fica equivalente ao problema de colorir, em que cores diferentes sinalizam horários diferentes. Algoritmos de colorir grafos são de grande interesse na ciência da computação e são usados para muitos problemas da vida real, apesar de eles provavelmente não serem usados para colorir mapas! – nosso cartógrafo pobre é apenas ficção.

Literalmente, existem milhares de outros problemas baseados em grafos. Alguns estão descritos em outras atividades, como na árvore de extensão mínima da Atividade 9 e o conjunto dominante da Atividade 14. Grafos são uma forma geral de representação de dados e podem ser usados para representar todos os tipos de situações, como mapas de estradas e cruzamentos, conexões entre átomos em uma molécula, caminhos que uma mensagem pode percorrer numa rede de computador, conexões entre componente de um circuito impresso e relações entre as etapas de um grande projeto. Por este motivo problemas envolvendo representação de grafos tem há tempos fascinado cientistas da computação.

Muitos desses problemas são muito difíceis – não difíceis conceitualmente, mas porque levam muito tempo para serem resolvidos. Por exemplo, para determinar a solução mais eficiente para um problema de grafo de tamanho médio – como encontrar a melhor maneira de agendar as aulas em uma escola com trinta professores e 800 alunos – poderia levar anos, até séculos, para um computador usando o melhor algoritmo conhecido. Até a solução ser descoberta, o problema poderia se tornar irrelevante – e isso se assumirmos que o computador não quebre ou se desgaste antes de terminar! Esses problemas só são resolvidos na prática porque nós nos contentamos em trabalhar com uma solução abaixo da ótima, ainda que boa. Se nós insistíssemos em garantir que a solução encontrada é a melhor de todas, o problema seria completamente inviável.

O tempo de processamento necessário para resolver problemas de colorir aumenta exponencialmente com o tamanho do grafo. Considere o problema de colorir o mapa. Ele pode ser resolvido tentando-se todas as formas possíveis de colorir o mapa. Nós sabemos que são necessárias no máximo quatro cores, então precisamos analisar todas as formas de distribuir as quatro cores no mapa. Se existem n países, existem \(4^n\) combinações. Esse número aumenta muito rapidamente: a cada país adicionado multiplicamos o número de combinações por 4 e assim quadruplicamos o tempo de processamento da solução. Mesmo se for inventado um computador que resolve o problema para cinquenta países em uma hora, adicionar um país levaria 4 horas, e nós só precisaríamos adicionar mais 10 países para fazer o computador levar mais de um ano para encontrar a solução. Este tipo de problema não vai desaparecer só porque continuamos inventando computadores cada vez mais rápidos.

Colorir grafos é um bom exemplo de problema cujo tempo de processamento para resolver cresce exponencialmente. Para versões bem simples do problema, como os mapas pequenos usados nesta atividade, encontrar a solução ótima é simples, mas assim que o número de países aumenta acima de aproximadamente 10, o problema se torna muito difícil de se resolver à mão, e com cem ou mais países até um computador pode levar muitos anos para testar todas as formas possíveis de colorir o mapa visando encontrar a maneira otimizada.

Muitos problemas na vida real são como este, mas precisam ser resolvidos de qualquer forma. Cientistas da computação usam métodos que fornecem respostas boas, mas não perfeitas. Estas técnicas heurísticas são frequentemente muito próximas da ótima, muito rápidas de processar e fornecem respostas que são suficientemente próximas para todos os objetivos práticos. Escolas podem tolerar usar uma sala de aula a mais do que seria necessária se a grade de horários fosse perfeita e talvez o cartógrafo pobre possa bancar uma cor a mais mesmo que não seja estritamente necessário.

Ninguém comprovou que não existe um jeito eficiente de resolver este tipo de problema em computadores convencionais, mas também ninguém comprovou que existe, e cientistas da computação são céticos sobre se um método eficiente será encontrado algum dia. Nós vamos aprender mais sobre este problema nas próximas duas atividades.

Para saber mais

O experimento “Com quantas cores posso pintar um mapa?” da coleção Matemática Multimídia trata do mesmo problema dessa atividade e conta com explicações e aprofundamentos em seu Guia do Professor. Além desse, a coleção possui outros recursos que abordam o tópico grafos. Você pode acessá-los aqui.

Soluções e dicas

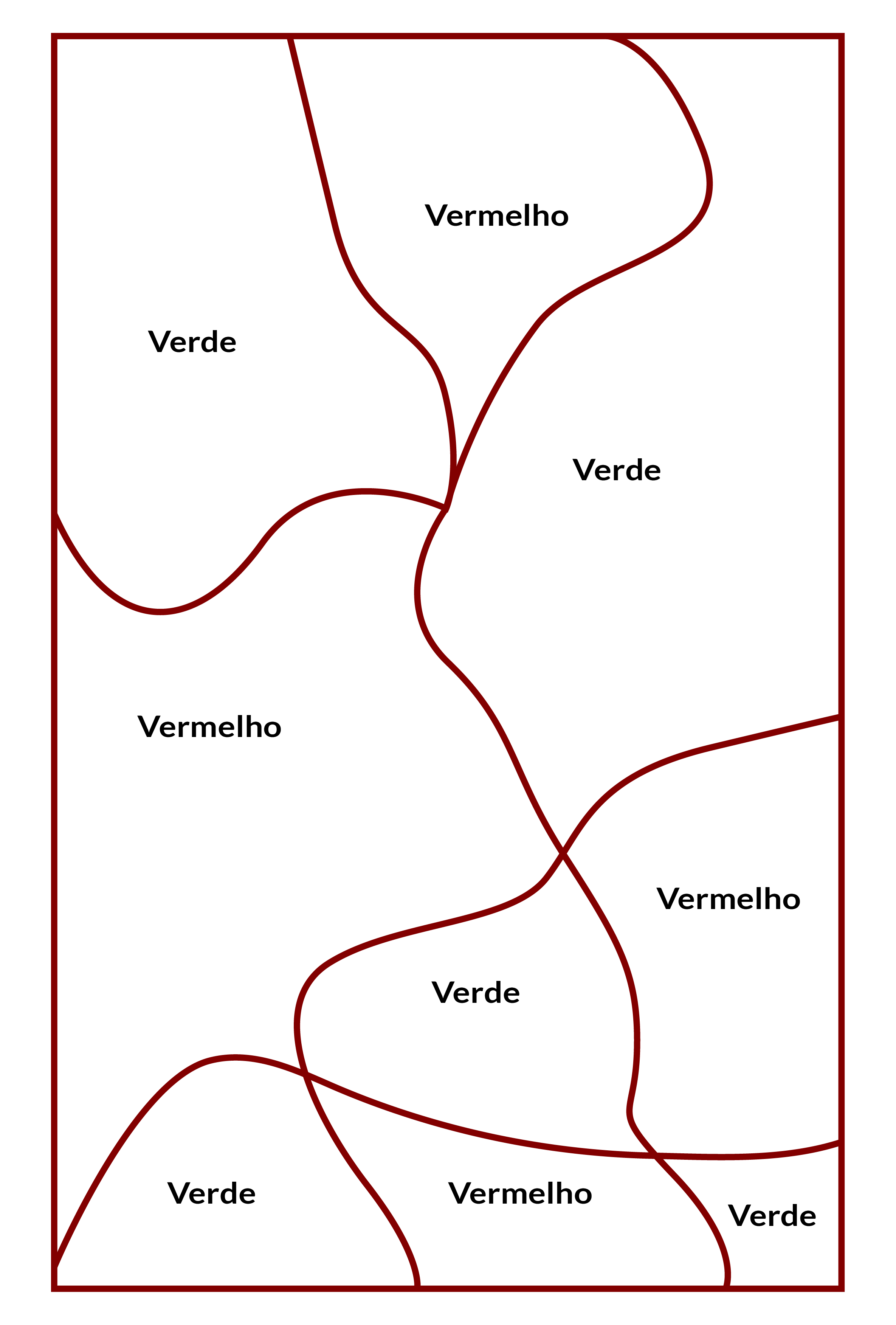
Esta é a única solução possível para o mapa da folha de atividade 1 (é claro que a escolha das cores cabe ao aluno, mas são necessárias apenas duas cores diferentes).

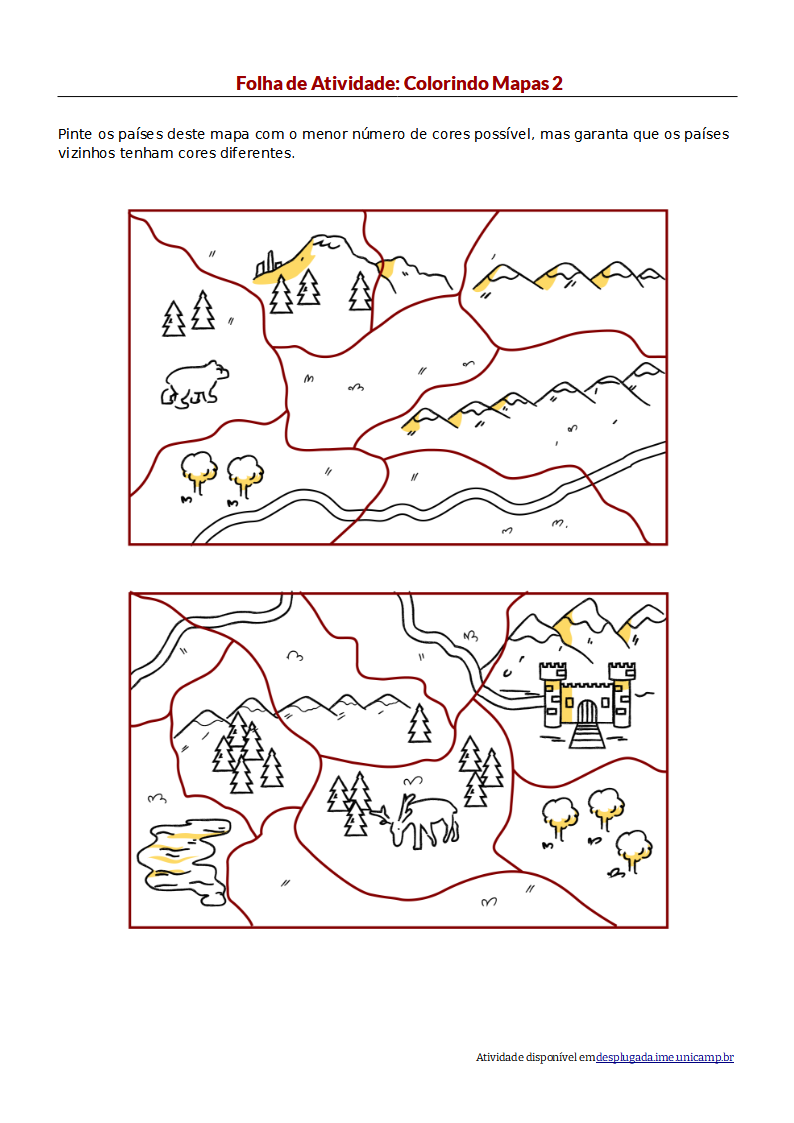
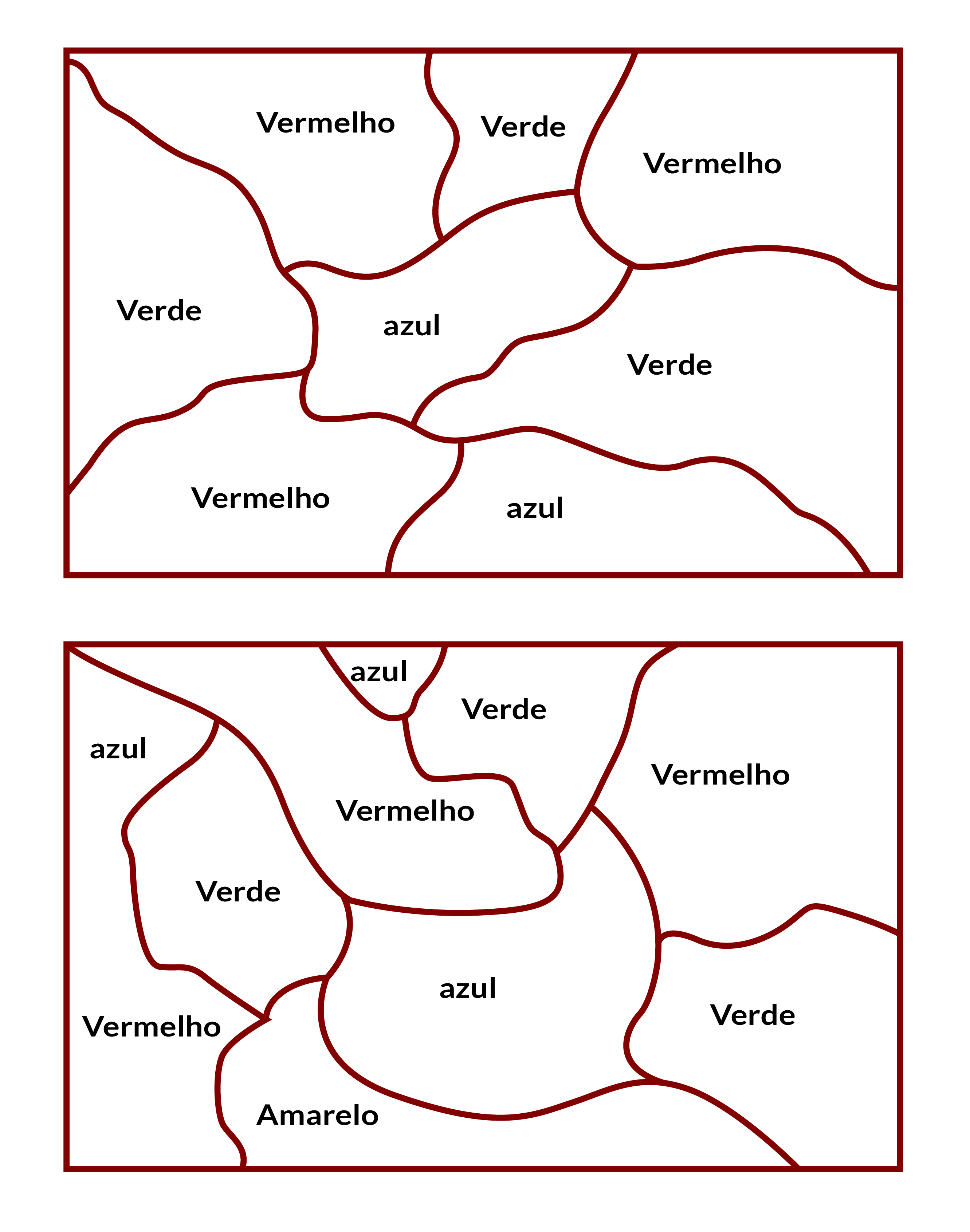
O mapa de cima da folha de atividade 2 pode ser colorido corretamente usando 3 cores diferentes, enquanto o de baixo precisa de 4. Aqui temos duas soluções possíveis.

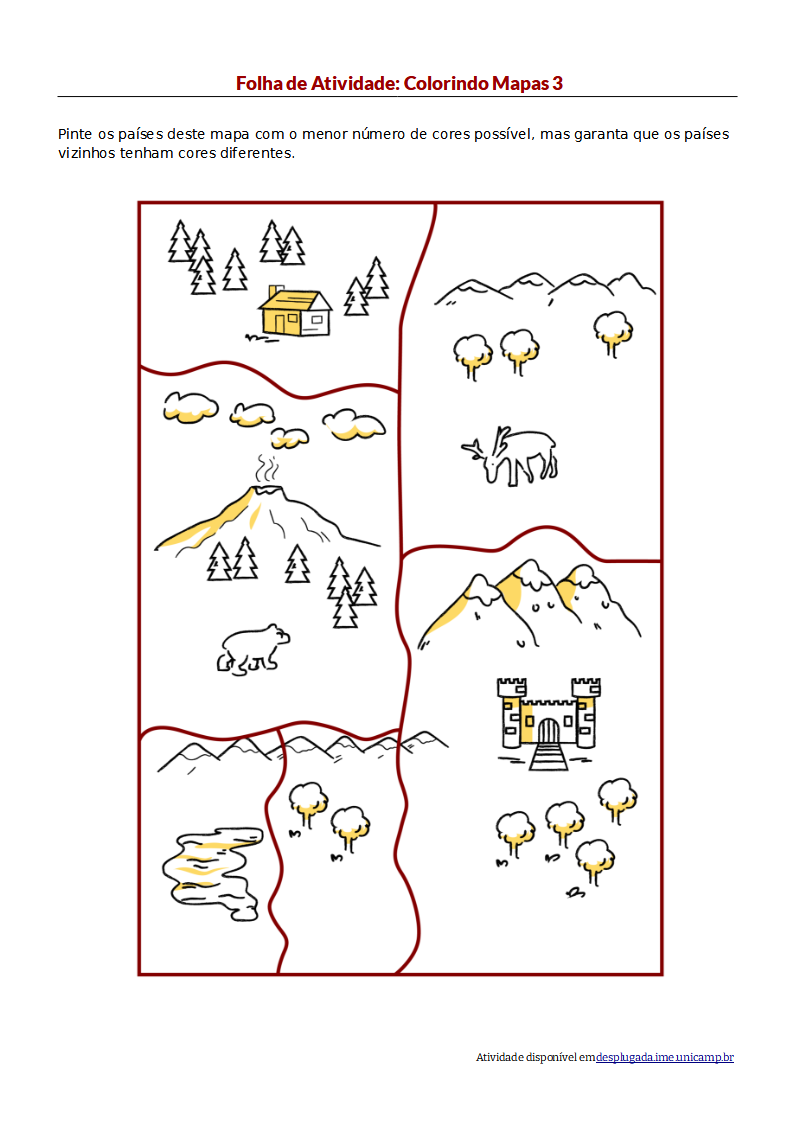
O mapa da folha de atividade 3 é um mapa simples de 3 cores, com uma possível solução mostrada abaixo.

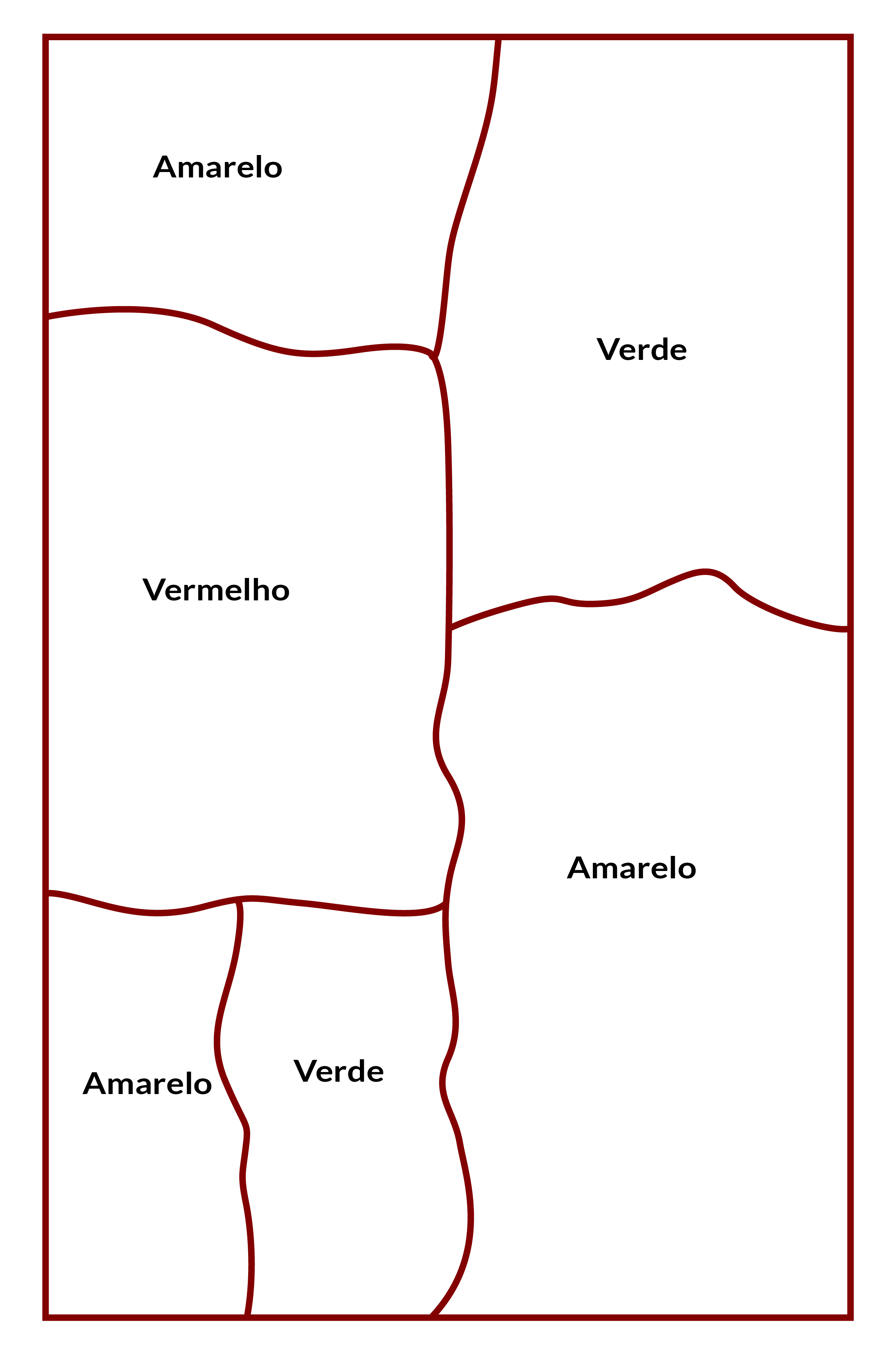
Resolução da folha de atividade 4 usando apenas duas cores (hachurado e branco).